Descriptive statistics vs Inferential statistics: In the field of statistics, there are two primary branches,
- Descriptive Statistics
- Inferential Statistics
Descriptive statistics vs Inferential statistics
The differences between the two branches are explained in this tutorial, as well as why each is helpful in certain scenarios.
Descriptive Statistics
In a word, descriptive statistics seeks to use summary statistics, graphs, and tables to describe a set of raw data.
When compared raw data values, descriptive statistics help you to understand a group of data considerably more quickly and readily.
Consider the following scenario: we have a set of raw data containing the test scores of 1,000 students at a specific school. The average test score, as well as the distribution of test scores, may be of interest.
We might find the average score and generate a graph to depict the distribution of results using descriptive statistics.
When analysing raw data, this makes it much easier to interpret the students test scores.
Descriptive Statistics in Common Forms
There are three different types of descriptive statistics that are frequently used
1. Statistical Summary: These are statistics that use a single number to summarise data. There are two types of summary statistics that are commonly used.
Measures of central tendency: these numbers indicate where a dataset’s centre is. The mean and the median are two examples.
Dispersion measures: these statistics describe how widely the values in the dataset are spread out. The range, interquartile range, standard deviation, and variance are some examples.
2. Diagrams: Graphs assist us in visualizing data. Boxplots, histograms, stem-and-leaf plots, and scatterplots are some of the most common graphs used to visualize data.
3. Tables: Tables can assist us in comprehending the distribution of facts. A frequency table is a type of table that tells us how many data values fall into various ranges.
Using Descriptive Statistics as an Example
The following example shows how descriptive statistics can be used in the real world.
Assume that 1,000 students at a particular school take the same test. Because we want to know how test scores are distributed, we employ the following descriptive statistics:
1. Statistics in Summary
The average is 85. This means that out of 1,000 students, the average test result is 85.
The median is 84. This means that half of all students received a score of 84 or higher, while the other half received a score of 84 or lower.
100 is the maximum number & 45 is the minimum. This means that each student received a maximum score of 100 and a minimum score of 45. The range is 55, which indicates the difference between the maximum and minimum values.
2. Diagrams
We may use a histogram – a sort of graphic that employs rectangular bars to indicate frequencies – to depict the distribution of test scores.
If we plot the data, we can see that the distribution of test results is essentially bell-shaped based on the histogram. The majority of the students scored in the 70s and 90s, with only a handful scoring above 95 and even fewer scoring below 50.
3. Tables
Making a frequency table is another simple technique to acquire a better grasp of the distribution of scores. The following frequency table, for example, indicates what proportion of students scored in certain ranges:
When we need to know what % of the data values go above or below a specified value, a frequency table comes in handy. For example, let’s say the school deems any score above 75 to be “acceptable.”
Statistical Inference
Inferential statistics, in a nutshell, uses a small sample of data to make conclusions about the wider population from which the sample was drawn.
For example, we would be interested in learning about the political preferences of a country’s millions of citizens.
However, surveying every single person in the country would take much too long and be practically sometimes not possible.
Instead, we’d conduct a smaller study of, say, 2,000 Americans and use the data to make conclusions about the entire population.
The entire assumption of inferential statistics is that we want to answer a question about a population, so we collect data for a small sample of that population and use the data to form conclusions about the population.
A Representative Sample’s Importance
To be confident in our ability to draw conclusions about a population from a sample, we must first ensure that we have a representative sample – that is, one in which the characteristics of the individuals in the sample roughly match those of the entire population.
Our sample should ideally be a “mini-version” of our population. So, if we wish to draw conclusions about a population of students made up of 50% females and 50% boys, our sample would be unrepresentative if it had 95% boys and just 5% girls.
If our sample is not representative of the entire population, we cannot confidently extrapolate the results from the sample to the entire population.
How to Get a Sample That Is Representative
To increase your chances of getting a representative sample, you should concentrate on two things:
1. Make sure you utilize a method of random sampling.
You can use a variety of random sampling methods to generate a representative sample, including:
A straightforward random sampling
A random sample was taken in a systematic manner
A random sample from a cluster
A stratified random sample of participants
Because every person in the population has an equal chance of being included in the sample, random sampling procedures tend to yield representative samples.
2. Double-check that your sample size is adequate.
Along with choosing an acceptable sampling procedure, make sure the sample is large enough to allow you to generalize your findings to a larger population.
To figure out how big your sample should be, think about the size of the population you’re investigating, the confidence level you want to use, and the allowable margin of error.
Fortunately, you can plug these variables into online calculators to determine the size of your sample.
Inferential Statistics in Common Forms
Inferential statistics can be divided into three types:
Hypothesis tests are a type of test that is used to determine whether or not a
Frequently, we’re looking for answers to inquiries concerning a population, such as:
Is the percentage of people in Ohio who support Candidate A greater than 50%?
Is the average height of a particular plant 15 inches?
Is there a difference in average height between students at School A and School B?
To answer these problems, we can utilize a hypothesis test, which allows us to draw inferences about populations based on data from a sample.
Confidence Intervals are a type of confidence interval.
We’re occasionally interested in estimating a population’s value. For instance, we might be curious about the average height of a particular plant species in Australia.
Instead of measuring every single plant in the country, we may gather a small sample of plants and measure each one individually.
The mean height of the plants in the sample can then be used to estimate the population’s mean height.
Our sample, on the other hand, is unlikely to yield an exact assessment of the population. Fortunately, we can account for this uncertainty by constructing a confidence interval, which specifies a range of values within which the true population parameter is most likely to fall.
For example, a 95 percent confidence interval of [13, 15] indicates that we’re 95% confident that the true mean height of this plant species is between 13 and 15 inches.
3. Regression
We’re sometimes curious about the relationship between two variables in a population.
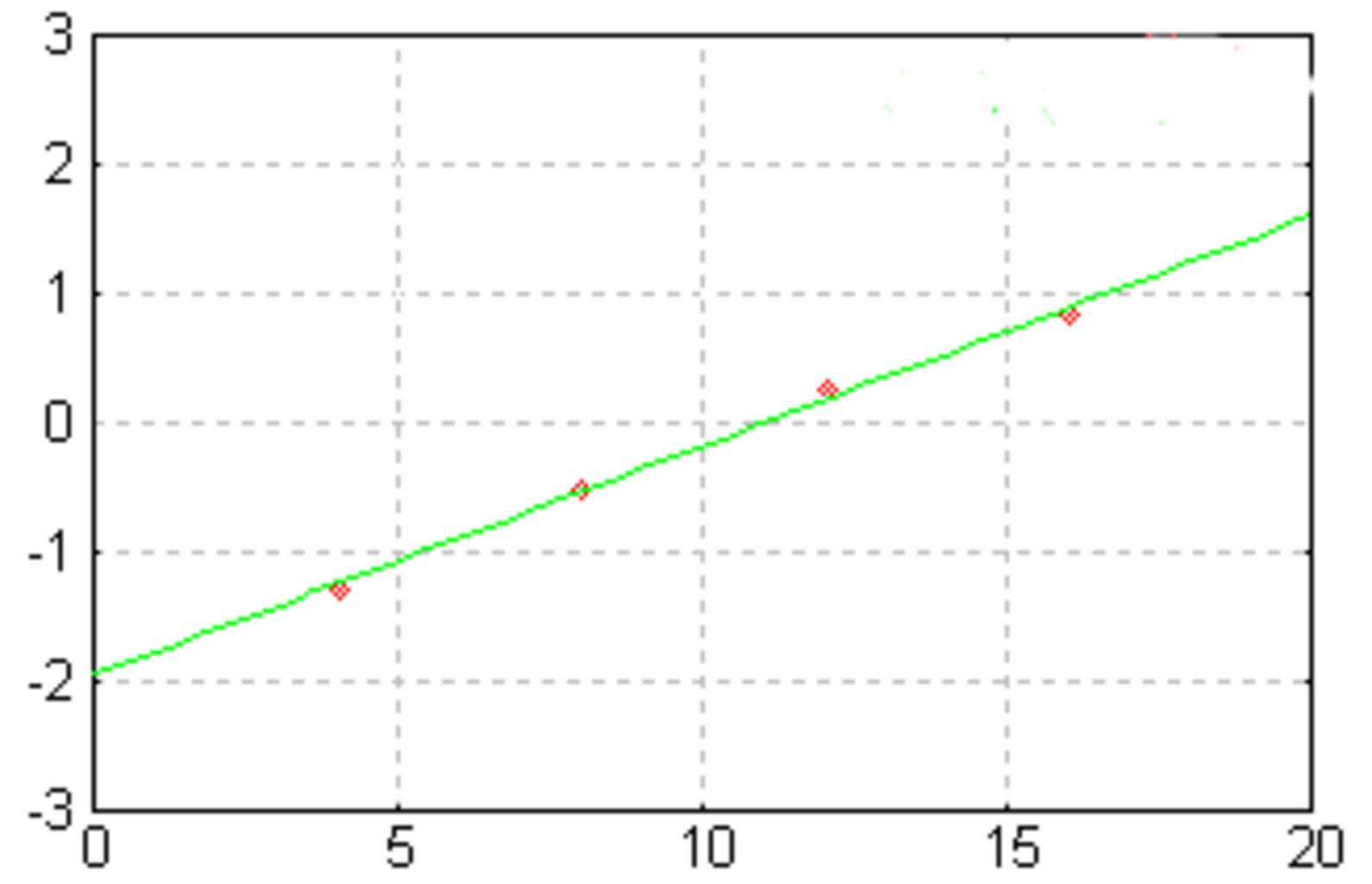
Let’s say we want to determine if the number of hours spent studying per week is related to test scores. We may use a technique known as regression analysis to address this question.
So, for 100 students, we might look at the number of hours studied as well as their exam scores and do a regression analysis to see whether there is a significant association between the two variables.
If the regression’s p-value is significant, we can conclude that there is a substantial association between these two variables in the entire student population.
Descriptive and inferential statistics are two types of statistics.
The following is a summary of the differences between descriptive and inferential statistics:
To characterize a data set, descriptive statistics employ summary statistics, graphs, and tables.
This is beneficial for quickly gaining an overview of a data set without having to go through all of the individual data values.
Samples are used in inferential statistics to make inferences about larger populations.
You can use one or more of the following approaches to answer a question about a population, depending on the question you wish to answer: hypothesis tests, confidence intervals, and regression analysis.
If you choose one of these methods, keep in mind that your sample must be representative of your population; otherwise, the conclusions you derive will be suspect.
How to Use the Multinomial Distribution in R? – Data Science Tutorial