One way ANOVA Example in R, the one-way analysis of variance (ANOVA), also known as one-factor ANOVA, is an extension of the independent two-sample t-test for comparing means when more than two groups are present.
The data is divided into numerous groups using one single grouping variable in one-way ANOVA (also called factor variable).
The basic premise of the one-way ANOVA test is described in this lesson, which also includes practical ANOVA test examples in R software.
Hypotheses for ANOVA tests:
The null hypothesis is that the means of the various groups are identical.
Alternative hypothesis: At least one sample mean differs from the rest.
You can use the t-test if you just have two groups. The F-test and the t-test are equivalent in this scenario.
The ANOVA test is described in this section.
Only when the observations are gathered separately and randomly from the population described by the factor levels can the ANOVA test be used.
Each factor level’s data is normally distributed.
The variance in these typical populations is similar. (This can be verified using Levene’s test.)
What is the one-way ANOVA test?
Assume we have three groups to compare (A, B, and C):
Calculate the common variance, often known as residual variance or variance within samples (S2within).
Calculate the difference in sample means as follows:
Calculate the average of each group.
Calculate the difference in sample means (S2between)
As the ratio of S2between/S2within, calculate the F-statistic.
Note that a lower ratio (ratio 1) suggests that the means of the samples being compared are not significantly different.
A greater ratio, on the other hand, indicates that the differences in group means are significant.
In R, visualize your data and do one-way ANOVA.
We’ll use the PlantGrowth data set that comes with R. It provides the weight of plants produced under two distinct treatment conditions and a control condition.
data <- PlantGrowth
We utilize the function sample n() [in the dplyr package] to get a sense of how the data looks.
The sample n() function prints out a random selection of observations from the data frame:
To display a sample at random
set.seed(123) dplyr::sample_n(data, 10)
weight group 1 5.87 trt1 2 4.32 trt1 3 3.59 trt1 4 5.18 ctrl 5 5.14 ctrl 6 4.89 trt1 7 5.12 trt2 8 4.81 trt1 9 4.50 ctrl 10 4.69 trt1
The column “group” is known as a factor in R, while the different categories (“ctr”, “trt1”, “trt2”) are known as factor levels. The levels are listed in alphabetical order.
levels(data$group) [1] "ctrl" "trt1" "trt2"
If the levels are not in the correct order automatically, reorder them as follows:
data$group <- ordered(data$group,
levels = c("ctrl", "trt1", "trt2"))The dplyr package can be used to compute summary statistics (mean and sd) by groups.
Calculate summary statistics by groups – count, mean, and standard deviation:
library(dplyr) group_by(data, group) %>% summarise( count = n(), mean = mean(weight, na.rm = TRUE), sd = sd(weight, na.rm = TRUE) )
group count mean sd <ord> <int> <dbl> <dbl> 1 ctrl 10 5.03 0.583 2 trt1 10 4.66 0.794 3 trt2 10 5.53 0.443
Visualize your information
Read R base graphs to learn how to utilize them. For an easy ggplot2-based data visualization, we’ll use the ggpubr R tool.
Best online course for R programming
install.packages("ggpubr")Visualize your data with ggpubr:
library("ggpubr")
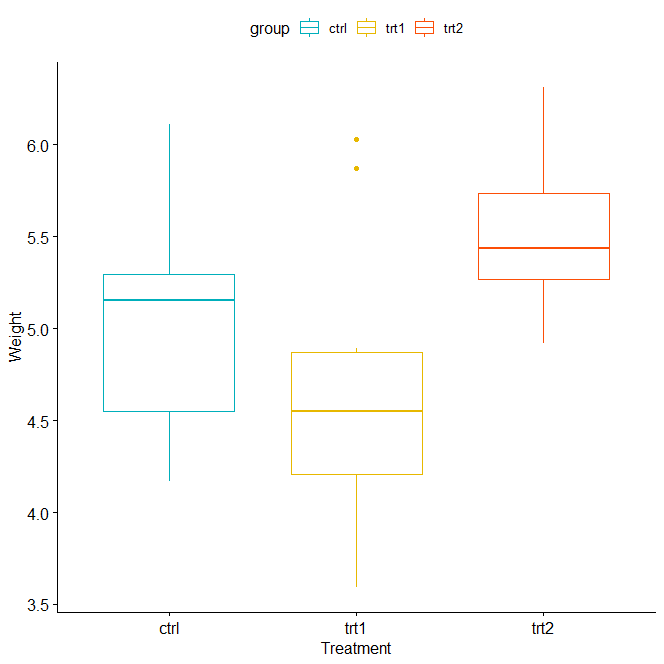
ggboxplot(data, x = "group", y = "weight",
color = "group", palette = c("#00AFBB", "#E7B800", "#FC4E07"),
order = c("ctrl", "trt1", "trt2"),
ylab = "Weight", xlab = "Treatment")
One-way ANOVA Test in R
Add error bars: mean_se
library("ggpubr")
ggline(data, x = "group", y = "weight",
add = c("mean_se", "jitter"),
order = c("ctrl", "trt1", "trt2"),
ylab = "Weight", xlab = "Treatment")
R’s one-way ANOVA test
Type the following scripts if you still want to utilise R basic graphs:
boxplot(weight ~ group, data = data,
xlab = "Treatment", ylab = "Weight",
frame = FALSE, col = c("#00AFBB", "#E7B800", "#FC4E07"))For plot means
library("gplots")
plotmeans(weight ~ group, data = data, frame = FALSE,
xlab = "Treatment", ylab = "Weight",
main="Mean Plot with 95% CI")
Calculate the one-way ANOVA test.
We want to see if the average weights of the plants in the three experimental circumstances vary significantly.
This question can be answered using the R function aov(). Summary of the function The analysis of the variance model is summarised using aov().
Perform an analysis of variance.
res.aov <- aov(weight ~ group, data = data)
Summary of the analysis
summary(res.aov)
Df Sum Sq Mean Sq F value Pr(>F) group 2 3.766 1.8832 4.846 0.0159 * Residuals 27 10.492 0.3886 --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
The columns F value and Pr(>F) in the output corresponding to the p-value of the test.
The results of one-way ANOVA testing should be interpreted.
We can conclude that there are significant differences between the groups highlighted with “*” in the model summary because the p-value is less than the significance level of 0.05.
Multiple pairwise comparisons between group means
A significant p-value implies that some of the group means are different in a one-way ANOVA test, but we don’t know which pairs of groups are different.
Multiple pairwise comparisons can be performed to see if the mean differences between certain pairs of groups are statistically significant.
Multiple Tukey pairwise comparisons
We can compute Tukey HSD (Tukey Honest Significant Differences, R function: TukeyHSD()) for doing numerous pairwise comparisons between the means of groups because the ANOVA test is significant.
The fitted ANOVA is passed to TukeyHD() as an input.
TukeyHSD(res.aov)
Tukey multiple comparisons of means
95% family-wise confidence level Fit: aov(formula = weight ~ group, data = data) $group diff lwr upr p adj trt1-ctrl -0.371 -1.0622161 0.3202161 0.3908711 trt2-ctrl 0.494 -0.1972161 1.1852161 0.1979960 trt2-trt1 0.865 0.1737839 1.5562161 0.0120064
lwr, upr: the lower and upper-end points of the confidence interval at 95 percent (default) p adj: p-value after multiple comparisons adjustment.
Only the difference between trt2 and trt1 is significant, as shown by the output, with an adjusted p-value of 0.012.
Using the multcomp package, perform several comparisons.
The function glht() [in the multcomp package] can be used to do multiple comparison processes for an ANOVA. General linear hypothesis tests are abbreviated as glht. The following is a simplified format:
library(multcomp)
glht(model, lincft)
model: a model that has been fitted, such as an object returned by aov ().
lincft() specifies the linear hypotheses that will be tested. Objects provided from the function mcp are used to specify multiple comparisons in ANOVA models ().
For a one-way ANOVA, use glht() to make numerous pairwise comparisons:
library(multcomp) summary(glht(res.aov, linfct = mcp(group = "Tukey")))
Simultaneous Tests for General Linear Hypotheses Multiple Comparisons of Means: Tukey Contrasts Fit: aov(formula = weight ~ group, data = my_data) Linear Hypotheses: Estimate Std. Error t value Pr(>|t|) trt1 - ctrl == 0 -0.3710 0.2788 -1.331 0.391 trt2 - ctrl == 0 0.4940 0.2788 1.772 0.198 trt2 - trt1 == 0 0.8650 0.2788 3.103 0.012 * --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 (Adjusted p values reported -- single-step method)
T-test with pairs
Pairwise comparisons across group levels with various testing corrections can also be calculated using the pairewise.t.test() function.
pairwise.t.test(data$weight, data$group p.adjust.method = "BH")
Pairwise comparisons using t tests with pooled SD
data: data$weight and data$group ctrl trt1 trt1 0.194 - trt2 0.132 0.013 P value adjustment method: BH
The output is a table of pairwise comparison p-values. The Benjamini-Hochberg method was used to alter the p-values in this case.
The validity of ANOVA assumptions should be checked.
The ANOVA test assumes that the data are normally distributed and that group variance is uniform. With certain diagnostic plots, we can verify this.
Examine the assumption of homogeneity of variance.
The residuals versus fits plot can be used to assess variance homogeneity.
There are no clear correlations between residuals and fitted values (the mean of each group) in the plot below, which is good. As a result, we can assume that the variances are homogeneous.
1: Variance homogeneity
plot(res.aov, 1)

ANOVA (one-way) Outliers are discovered in R Points 17, 15, 4, which can have a significant impact on normality and homogeneity of variance.
To meet the test assumptions, it can be beneficial to remove outliers.
The homogeneity of variances can also be checked using Bartlett’s or Levene’s tests.
Levene’s test is recommended since it is less sensitive to deviations from normal distribution. The leveneTest() method [from the car package] will be used:
library(car) leveneTest(weight ~ group, data = data)
Levene’s Test for Homogeneity of Variance (center = median)
Df F value Pr(>F) group 2 1.1192 0.3412 27
The p-value is not less than the significance level of 0.05, as seen in the output above. This indicates that there is no indication that the variance across groups is statistically significant.
As a result, we can infer that the variations in the different treatment groups are homogeneous.
Relaxing the premise of homogeneity of variance
The traditional one-way ANOVA test assumes that all groups have similar variances. The homogeneity of variance assumption was fine in our case: the Levene test was not significant.
In a circumstance where the homogeneity of variance assumption is violated, how do we save our ANOVA test?
An alternate approach (e.g., the Welch one-way test) that does not necessitate the use of assumptions in the one-way function. test().
ANOVA test with no equal variance assumption
oneway.test(weight ~ group, data = data)
one-way analysis of means (not assuming equal variances)
data: weight and group F = 5.181, num df = 2.000, denom df = 17.128, p-value = 0.01739
Pairwise t-tests with no assumption of equal variances
pairwise.t.test(data$weight, data$group, p.adjust.method = "BH", pool.sd = FALSE)
Pairwise comparisons using t-tests with non-pooled SD
data: data$weight and data$group ctrl trt1 trt1 0.250 - trt2 0.072 0.028 P value adjustment method: BH
Examine the presumption of normality.
Residuals normality plot The residuals quantiles are displayed against the normal distribution quantiles in the graph below. Also plotted is a 45-degree reference line.
The residuals’ normal probability plot is used to verify that the residuals are normally distributed. It should be about in a straight line.
2: Normality
plot(res.aov, 2)

ANOVA (one-way) R-based test
We can infer normality because all of the points lie roughly along this reference line.
Extract the residuals
aov_residuals <- residuals(object = res.aov )
Run Shapiro-Wilk test
Shapiro-Wilk normality test
shapiro.test(x = aov_residuals )
data: aov_residuals W = 0.96607, p-value = 0.4379
The Shapiro-Wilk test on the ANOVA residuals (W = 0.96, p = 0.43), which finds no evidence of normality violation, supports the previous conclusion.
ANOVA test with a non-parametric alternative
The Kruskal-Wallis rank-sum test is a non-parametric alternative to one-way ANOVA that can be employed when the ANOVA assumptions are not met.
kruskal.test(weight ~ group, data = data)
Kruskal-Wallis rank-sum test
data: weight by group Kruskal-Wallis chi-squared = 7.9882, df = 2, p-value = 0.01842